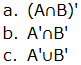Topic 10: Sets - Mathematics Study Notes Form II

Welcome to our website darasahuru.co.tz, in this website you will find Topic 10: Sets - Mathematics Study Notes Form II, Form Two Sets Notes, Mathematics Notes PDF, Mathematics Notes For Form Two Free Download PDF.

Topic 10: Sets - Mathematics Study Notes Form II

Sets

Forget everything you know about number and forget that you even know what a number is.

This is where mathematics starts. Instead of mathematics with numbers we will think about mathematics with things.

The word set means collection of related things or objects. Or, things grouped together with a certain property in common. For example, the items you wear: shoes, socks, hat, shirt, pants and so on.

This is called a set. A set notation is simple, we just list each element or member (element and member are the same thing), separated by comma, and then put some curly brackets around the whole thing. See an example below:

The Curly brackets are sometimes called “set brackets” or “Braces”.

 

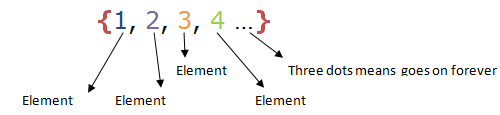
Sets are named by capital letters. For example; A = {1, 2, 3, 4 …} and not a = {1, 2, 3, 4, …}.

To show that a certain item belongs to a certain set we use the symbol ∈.

For example if set A = {1, 2, 3, 4} and we want to show that 1 belongs to set A (is an element of set A) we write 1∈A.

To show the total number of elements that are in a given set, say set A, we use the symbol n(A). Using our example A = {1, 2, 3, 4}, then, the total number of elements of set A is 4. Symbolically , we write n(A) = 4

Description of a Set

A Set Define a set

We describe sets either by using words, by listing or by Formula. For example if set  A is a set of even numbers, we can describe it as follows:

1. By using words: A = {even numbers}
2. By listing: A = {2, 4, 6, 8, 10,…}
3. By Formula: A = {x: x = 2n, where n = 1,2,3,…} and is read as A is a set of all x such that x is an even number.

Example 1

Describe the following set by listing: N is a set of Natural numbers between 0 and 11

Solution

N = {1,2,3,4,5,6,7,8,9,10}

Example 2

Write the following named set using the formula: O is a set of Odd numbers:

Solution

O = {x: x = 2n – 1, whereby n = 1,2,3….}

 

Example 3

Write the following set in words: W = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

Solution

W = {whole numbers} or W is a set of whole numbers.

The Members of a Set

List the members of a set

The objects in a set are called the members of the set or the elements of the set.

A set should satisfy the following:

1. The members of the set should be distinct. (not be repeated)
2. The members of the set should be well-defined. (well-explained)

Example 4

In question 1 to 3 list the elements of the named sets.

1. A={x: x is an odd number <10}
2. B={days of the week which begin with letter S}
3. C={prime numbers less than 13}

Solution

1. A={1,3,5,7,9}

2. B={Saturday,Sunday}

3. C={2,3,5,7,11}

Naming a Set

Name a set

To describe a small set, we list its members between curly brackets {, }:

• {2, 4, 6, 8}
• { England, France, Iran, Singapore, New Zealand }
• { David Beckham } {}
• (the empty set, also written ∅)

We write a ∈ X to express that a is a member of the set X. For example 4 ∈ {2, 4, 6, 8}. a /∈ X means a is not a member of X.

Differentiate Sets by Listing and by Stating the Members

Distinguish sets by listing and by stating the members

By Stating the members: A = {even numbers}

By listing: A = {2, 4, 6, 8, 10,…}

Types of Sets

A Universal Set and an Empty Set

Define a universal set and an empty set

Universal set

This is a set that contains everything that we are interested in. The symbol for universal set is μor

U. for example, the set of Integers contains all the elements of sets

such as odd numbers, prime numbers, even numbers, counting numbers and

whole numbers. In this example the set of integers is the Universal set.

Another example of a Universal set is a Set of all English Alphabets which

contains all elements of a set of vowels and set of Consonants.

Empty set or Null set: is a set with no elements. There aren’t any elements in it. Not one. Zero elements. For example; A set of Countries South of the South Pole.

It is represented by Øor {}.

The Difference Between Finite and Infinite Sets

Distinguish between finite and infinite sets

Finite sets: is a set which its elements can be counted.

We can say how many members are there. For example; a set B is a set of numbers between 1 and 7. When we list the elements, then set B = {2,3,4,5,6}. So, there 5 elements. This set is called finite set.

Infinite set: this is a set whereby we cannot count the number of elements of the set.

We cannot tell how many members are there in a set. For example; A is a set of all real numbers. Real numbers are all positive and negative numbers including fractions. We cannot count the members of a set of real numbers.

Another example; B = {1,2,3,…}. Three dots means go on or infinite, we will go on with no end. This types of sets are called infinite sets.

The Difference Between Equivalent and Equal Sets

Distinguish between equivalent and equal sets

Equivalent sets:

Two sets are said to be equivalent if their members match exactly. For example; if A = {a, b, c, d} and B = {w, x, y, z} the two sets match like this:

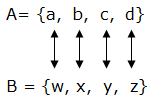
Generally, two sets are equivalent if n(A) = n(B). Symbolically we write A ≡B which means A is equivalent to B.

Equal sets:

If two sets are equivalent and their members are alike, then the two sets are said to be equal. For example; if A = {a, b, c, d} and B = {c, a, b, d} then the two sets are equal since a is in set A and in set B, b is in set A and in set B, c is in set A and in set B and d is in set A and in B. Also, numbers of elements of the both sets are equal.

Therefore A = B (set A is equal to set B)

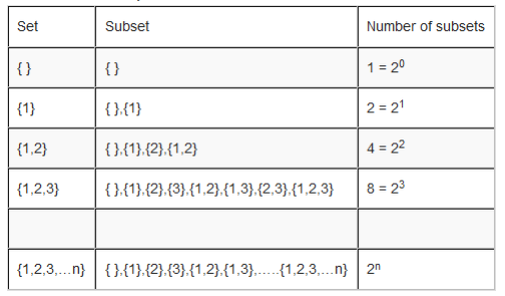
Subsets

A Subset

Define a subset

When we define a set, if we take piece of that set, we can form what is called a subset. For example; if we have a set {a, b, c, d, e}, a subset of this is {b, c, d}. Another subset is {a, b} or even another subset is {e} or {d} and so

on. 

However {a, f} is not a subset since it contains an element (f) which it is not in the parent set. 

Generally, A is a subset of B if and only if every element of A is in B. symbolically we write A⊂B (means A is a subset of B).

Subsets of a Given Set

List subsets of a given set

For example; if A = {1, 2, 3, 4}, B = {1, 2, 3} and C = {1, 2, 3, 4} then, B is a proper subset of A i. e. B⊂A and C is an improper subset of A i.e. C⊆A.

Important note: an Empty set is a subset of any set. 

The Difference between Proper and Improper Subsets

Distinguish between proper and improper subsets

If every element in A is also in B, and there exist at least one element in B that is not in A, we say that A is Proper subset of B.

And if every element in A is in B, and there is no element in B that is not in A, we say that A is an improper subset of B and we write A = B or symbolically we write A⊆B or B⊆A.

The Number of Subsets in a Set

Calculate the number of subsets in a set

Consider an example below:

When you look at the table, you will see that the number of subsets can be obtained by 2 raised to the number of elements of the set under consideration. Therefore, the formula for finding the number of subsets of a set with n elements is given by 2ⁿ, n is a number of elements of a set.

Example: How many subsets are there in set A = {Red, White, Yellow}. List them. Solution: case 1, number of subsets Set A has 3 elements. 

But Number of subsets = 2ⁿ, so number of subsets of set A = 2³ = 8

Therefore set A has 8 subsets

Case 2: list of subsets.

The subsets of set A are: { },{Red},{White},{Yellow},{Red,White},{Red,Yellow},{White,Yellow}, {Red,White,Yellow}.

Operations With Sets

Union of Two Sets

Find union of two sets

When elements of two or more sets are put together with no repetition, we get another set which is a union set. The symbol for union is ∪.

For example; if A = {a,b} and B = {a,b,c,d,e}, then A∪B = {a,b,c,d,e}.

Another example; if A = {a,b,c} and B = {5,6,2,4}, find A∪B.

Solution

A∪B = {a,b,c,5,6,2,4}

The Compliment of a Set

Find the compliment of a set

Complement means ‘everything that is not’. For example; if A is a subset of a universal set, the elements of a universal set that are not in A are the complements of set A. complement of a set is denoted by C. So complement of set A is written as A^c. Or A′.

For example; if ∪= {0,1,2,3,4,5,6,7,8,9,} and A = {1,3,5,7,9}. Find A^c.

Solution

We are required to find elements which are not in A but are in ∪.

Therefore, A^c= {2,4,6,8}.

The Number of Elements in the Union and Intersection of two Sets

Find the number of elements in the union and intersection of two sets

If A = {a,b,c} and B = {5,6,2,4}, find A∪B.

Solution

A∪B = {a,b,c,5,6,2,4}

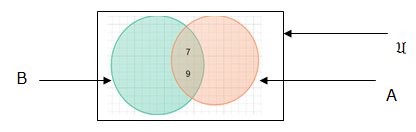
Inters ection

If we have two sets A and B and we decide to form a new set by taking only common elements from both sets i.e. elements which are found both in A and B. This new set is called intersection of set A and B. the symbol for intersection is ∩. Intersection of sets A and B is denoted by A∩B.for example; if A = {a,b,d,e} and B = {a b,d,f,g} then, the common elements are: a, b and d. 

Therefore, A∩B = {a,b,d}. Another example; if A = {1,3,5,7,9} and B = {2,4,6,8}. Find A∩B.

Answer

When you take a look at our sets, you will notice that there is no even a single element which is in common. Therefore, intersection of set A and B is an Empty set i.e. A∩B = or { }.

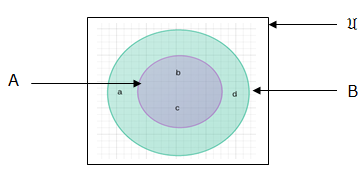
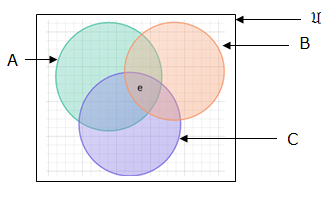
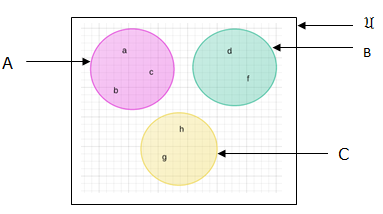
Vein Diagrams

Representing Sets by using Venn Diagrams

Represent a sets by using venn diagrams

The diagrams are oval shaped. They we named after John venn, an English Mathematician who introduced them. For example A = {1,2,3} in venn

diagram can be represented as follows:

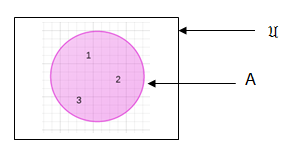
is a universal set which can be a set of counting numbers and A is a subset of it.

If we have two sets, say Set A and B and these sets have some elements in common and we are supposed to represent them in venn diagrams, their ovals will overlap. 

For example if A = {a,b,c,d,e,} and B = {a,e,i,o,u} in venn diagrams they will look like this:

If the two sets have no elements in common, then the ovals will be separate. For example; if A = {1,2,3} and B = {5,6}. In venn diagram they will appear like here below:

If we have two sets, A and B and set A is a subset of set B then the oval for set A will be inside the oval of set B. for example; if A = {b,c} and B = {a,b,c,d} then in venn diagram it will look like this:

If we have to represent the union or intersection of two or more sets using venn diagrams, the appearance of the venn diagrams will depend on whether the sets under consideration have some elements in common or not.

Information from Venn Diagrams

Interpret information from venn diagrams

Case 1: sets with elements in common.

Example 1: If A = {5,6,7,9,10} and B = {3,4,7,9,11} represent A union B and A intersection B in venn diagrams.

Solution

Case 1: A union B

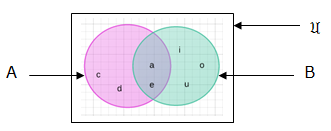
Case 2: A intersection B

Example 2:

A = {a,b,c,d,e,f}, B = {a,e} and C = {b,c,e,d}. Represent in venn diagrams A∪B∪C and A∩B ∩C.

Solution: case 1. A∪B∪C

Case 2: A ∩B∩C

Case 2:

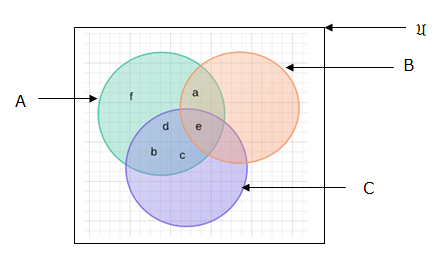
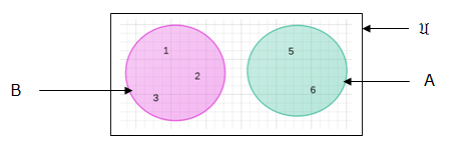
sets with no elements in common:

For example; A = {a,b,c,}, B = {d,f}, C = {h,g} on venn diagram will appear like this:

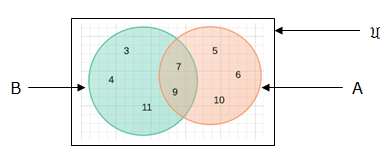
Number of elements in two sets say set A and B i.e. n(A∪B) is given by: n(A∪B) = n(A) + n(B) – n(A ∩B)

proof: consider the venn diagram below:

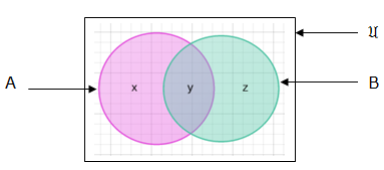
From our venn diagram:

n(A) = x + y, n(B) = y + z, n(A∩B) = y and n(A∪B) = x + y + z thus;

n(A) + n(B) = (x + y) + (y + z)

= (x + y + z) + y

but x + y + z = n(A ∪B) and n(A∩B) = y

so,

n(A) + n(B) = n(A∪B) + n(A∩B)

make n(A∪B) be the subject of the formula

For example; if n(A) = 15, n(A∩B) = 3 and n(A∪B) = 24. Find n(B)

Soln;

Recall that: n(A∪B) = n(A) + n(B) – n(A∩B)

n(B) = n(A∪B) + n(A∩B) – n(A)

= 24 + 3 – 15

n(B) = 12

Therefore, n(B) = 12

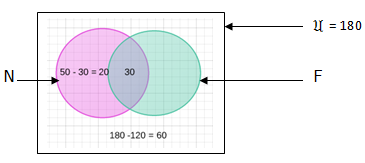
Word problems

For example; at Mtakuja primary school there are 180 pupils. If 120 pupils like one of the sports, either netball or football and 50 pupils likes netball while 30 pupils likes both netball and football. How many pupils

1. likes football.
2. Likes neither of the sport

Solutions.

Let be the universal set

N be the set of pupils who likes netball

F be the set of pupils who likes football

Thus,

n(F) = ?

n(N∩F) = 30

n(N∪F) = 120

n(μ) = 180

But we know that n(N∪F) = n(N) + n(F) – n(N∩F)

Thus, n(F) = n(N∪F) + n(N∩F) – n(N)

= 120 + 30 – 50

n(F) = 100

Therefore there are 100 pupils who likes football.

2. We have a total of 180 pupils at Mtakuja primary school

But only 120 pupils likes one of either the sport. so, those who likes neither of the sport will be 180 – 120 = 50

Therefore 50 pupils likes neither of the sport.

Alternatively: by using venn diagram

n(F) only = 120 – 30 -20 = 70

n(F) = those who likes both netball and football + those who likes football only

n(F) = 30 + 70 = 100

Therefore, there 100 pupils who likes football.

Exercise 1

1. If A = {Red,White,Blue} show by using symbol that Red, White and Blue are members of set A.

2. List the elements of set B if B is a set of counting numbers.

3. Which of the following sets are finite, infinite or empty sets.

A = {y:y is an odd number}

B = {1,3,7,…35}

C = { }

D = {Maths, Biology, Physics, Chemistry}

E = {Prime numbers between 31 and 37}

F = {….-2,-1,0,1,2,…}

4. If A = {1,4,9,16,25,36}, B = {1,4,9} and C = {1,3,4}, which of the following statement is true:

1. A⊂B
2. B⊂A
3. A⊆C
4. C⊆B

5. How many subsets are there in set A = {f,g,I,k,m,n}? List them all.

6.If A = {all letters of English Alphabets} and B = {c,d,g,h}.List the elements of B′.

7. Let B be a set of whole numbers and C a set of prime numbers found in a set of whole numbers, using venn diagram show B∩C.

8. Draw a venn Diagram and show by shading the required region:

9. If n(A) = 90, n(B) = 120 and n(A∩B) = 45. Find:

1. n(A∪ B)
2. n(B) only.
3. n(A) only.

10. In a certain meeting 40 people drank juice, 25 drank soda and 20 drank both juice and soda. How many people were in the meeting, assuming that

each person took juice or soda?